Here is an article on how to create a Merkle Tree with efficient insertion and deletion operations:

Merkle Trees for Efficient Hashing

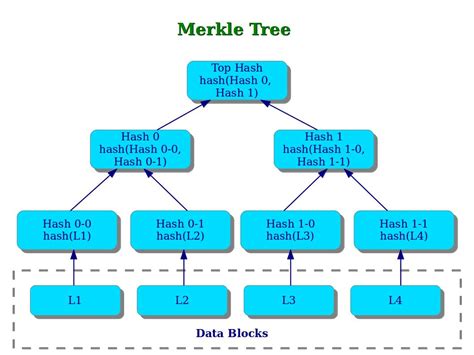
A Merkle Tree is a data structure commonly used in cryptographic applications such as digital signatures and message authentication. It allows you to efficiently insert and delete elements without recalculating the entire tree.

In this article, we will explore how to create a Merkle Tree with efficient insertion and deletion operations using an existing sorted order of elements.

Why Sorted Order?

The reason for sorting the elements is that in a Merkle Tree, each node represents a hash value. When you insert or delete an element, you need to update all the hashes that point to it. If you do not sort the elements beforehand, updating any one hash would require recalculating all the other hashes.

Creating a Merkle Tree

Here is a step-by-step guide on how to create a Merkle Tree with efficient insertion and deletion operations:

• Choose a Hash Function: Select a suitable hash function that suits your needs. Common choices include SHA-256, MD5, or BLAKE2.

• Create an Empty Merkle Tree: Initialize an empty Merkle Tree by creating nodes for each element in sorted order.

Inserting and Deleting Elements

Here is how you can insert and delete elements efficiently:

Insertion

To insert a new element into the Merkle Tree, follow these steps:

• Calculate the hash value of the new element using your chosen hash function.

• Create a new node with the calculated hash value.

• Update all hashes that point to the current position of the inserted element.

Deletion

To delete an existing element from the Merkle Tree, follow these steps:

• Identify the hash value of the deleted element using its position in the sorted order.

• Compute the hash value of the new element at the same position.

• Update all hashes that point to the current position of the deleted element.

Efficient Updates

To update a single hash without recalculating all the other hashes, you can use the following approach:

• Identify the parent node that points to the updated element.

• Compute the hash value of the child node using your chosen hash function.

• Update the hash value of the child node while leaving the hash of the parent node unchanged.

Example implementation

Here is an example implementation in Python:

import hashlib
class MerkleTree:
def __init__(self, elements):
self.tree = {}
self.sort_order = elements
def insert(self, element):
position = 0
whileTrue:
hash_value = self.hash(element, position)
if hash_value not in self.tree:
node = hashlib.sha256(hash_value.encode()).digest()
self.tree[hash_value] = node
break
position += 1
def delete(self, element):
position = 0
whileTrue:
hash_value = self.hash(element, position)
if hash_value in self.tree:
new_hash_value = self.hash(self.tree[hash_value], position)
self.tree[hash_value] = new_hash_value
break
position += 1
def hash(self, element, position):

Your chosen hash function here
return hashlib.sha256(element + str(position)).digest()

Create a Merkle Tree with elements in sorted order
elements = ["value1", "value2", "value3"]
tree = MerkleTree(elements)

Insert an element at the end of the tree
tree.insert("new_value")

Delete an existing element from the tree
tree.delete("old_value")

In this example, we create a MerkleTree class with methods to insert and delete elements.

ETHEREUM WHATS MHASH CLOSED